Ćuk converter
The Ćuk converter (pronounced Chook, sometimes incorrectly spelled Cuk, Čuk or Cúk) is a type of DC-DC converter that has an output voltage magnitude that is either greater than or less than the input voltage magnitude.
The non-isolated Ćuk converter can only have opposite polarity between input and output. It uses a capacitor as its main energy-storage component, unlike most other types of converters which use an inductor. It is named after Slobodan Ćuk of the California Institute of Technology, who first presented the design.[1]
Contents |
Non-isolated Ćuk converter
There are variations on the basic Cuk converter. For example, the coils may share single magnetic core, which drops the output ripple, and adds efficiency. Because the power transfer flows continuously via the capacitor, this type of switcher has minimized EMI radiation. The Cuk converter enables the energy flow bidirectionally, by adding a diode and a switch.
Operating Principle
A non-isolated Ćuk converter comprises two inductors, two capacitors, a switch (usually a transistor), and a diode. Its schematic can be seen in figure 1. It is an inverting converter, so the output voltage is negative with respect to the input voltage.
The capacitor C is used to transfer energy and is connected alternately to the input and to the output of the converter via the commutation of the transistor and the diode (see figures 2 and 3).
The two inductors L1 and L2 are used to convert respectively the input voltage source (Vi) and the output voltage source (Co) into current sources. Indeed, at a short time scale an inductor can be considered as a current source as it maintains a constant current. This conversion is necessary because if the capacitor were connected directly to the voltage source, the current would be limited only by (parasitic) resistance, resulting in high energy loss. Charging a capacitor with a current source (the inductor) prevents resistive current limiting and its associated energy loss.
As with other converters (buck converter, boost converter, buck-boost converter) the Ćuk converter can either operate in continuous or discontinuous current mode. However, unlike these converters, it can also operate in discontinuous voltage mode (i.e., the voltage across the capacitor drops to zero during the commutation cycle).
Continuous mode
In steady state, the energy stored in the inductors has to remain the same at the beginning and at the end of a commutation cycle. The energy in an inductor is given by:
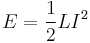
This implies that the current through the inductors has to be the same at the beginning and the end of the commutation cycle. As the evolution of the current through an inductor is related to the voltage across it:
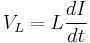
it can be seen that the average value of the inductor voltages over a commutation period have to be zero to satisfy the steady-state requirements.
If we consider that the capacitors C and Co are large enough for the voltage ripple across them to be negligible, the inductor voltages become:
- in the off-state, inductor L1 is connected in series with Vi and C (see figure 2). Therefore
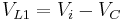 . As the diode D is forward biased (we consider zero voltage drop), L2 is directly connected to the output capacitor. Therefore
. As the diode D is forward biased (we consider zero voltage drop), L2 is directly connected to the output capacitor. Therefore 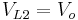
- in the on-state, inductor L1 is directly connected to the input source. Therefore
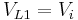 . Inductor L2 is connected in series with C and the output capacitor, so
. Inductor L2 is connected in series with C and the output capacitor, so 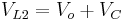
The converter operates in on-state from t=0 to t=D·T (D is the duty cycle), and in off state from D·T to T (that is, during a period equal to (1-D)·T). The average values of VL1 and VL2 are therefore:
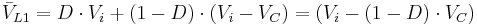
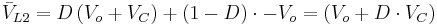
As both average voltage have to be zero to satisfy the steady-state conditions we can write, using the last equation:
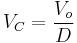
So the average voltage across L1 becomes:
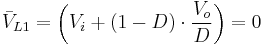
Which can be written as:
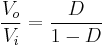
It can be seen that this relation is the same as that obtained for the Buck-boost converter.
Discontinuous mode
Like all DC-DC converters Cuk converters rely on the ability of the inductors in the circuit to provide continuous current, in much the same way a capacitor in a rectifier filter provides continuous voltage. If this inductor is too small or below the "critical inductance", then the current will be discontinuous. This state of operation is usually not studied in much depth, as it is not used beyond a demonstrating of why the minimum inductance is crucial.
The minimum inductance is given by:
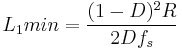
Where 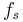 is the switching frequency.
is the switching frequency.
Current
Voltage
Related structures
Inductor coupling
Instead of using two discrete inductor components, many designers implement a coupled inductor Ćuk converter, using a single magnetic component that includes both inductors on the same core. The transformer action between the inductors inside that component gives a coupled inductor Ćuk converter lower output ripple than a Ćuk converter using two independent discrete inductor components.[2]
Single-ended primary-inductance converter (SEPIC)
A SEPIC converter is able to step-up or step-down the voltage.
References
- ^ Ćuk, Slobodan; Middlebrook, R. D. (June 8, 1976). "A General Unified Approach to Modelling Switching-Converter Power Stages" (PDF). Proceedings of the IEEE Power Electronics Specialists Conference (Cleveland, OH.): pp.73–86. http://www.ee.bgu.ac.il/~kushnero/temp/guamicuk.pdf. Retrieved 2008-12-31.
- ^ The Four Boostbuck Topologies